Pascal Jr. Tikeng Notsawo

Pascal Jr. Tikeng Notsawo

PhD Student at UdeM & Mila

Grokking Beyond the Euclidean Norm of Model Parameters

less than 1 minute read

Published:

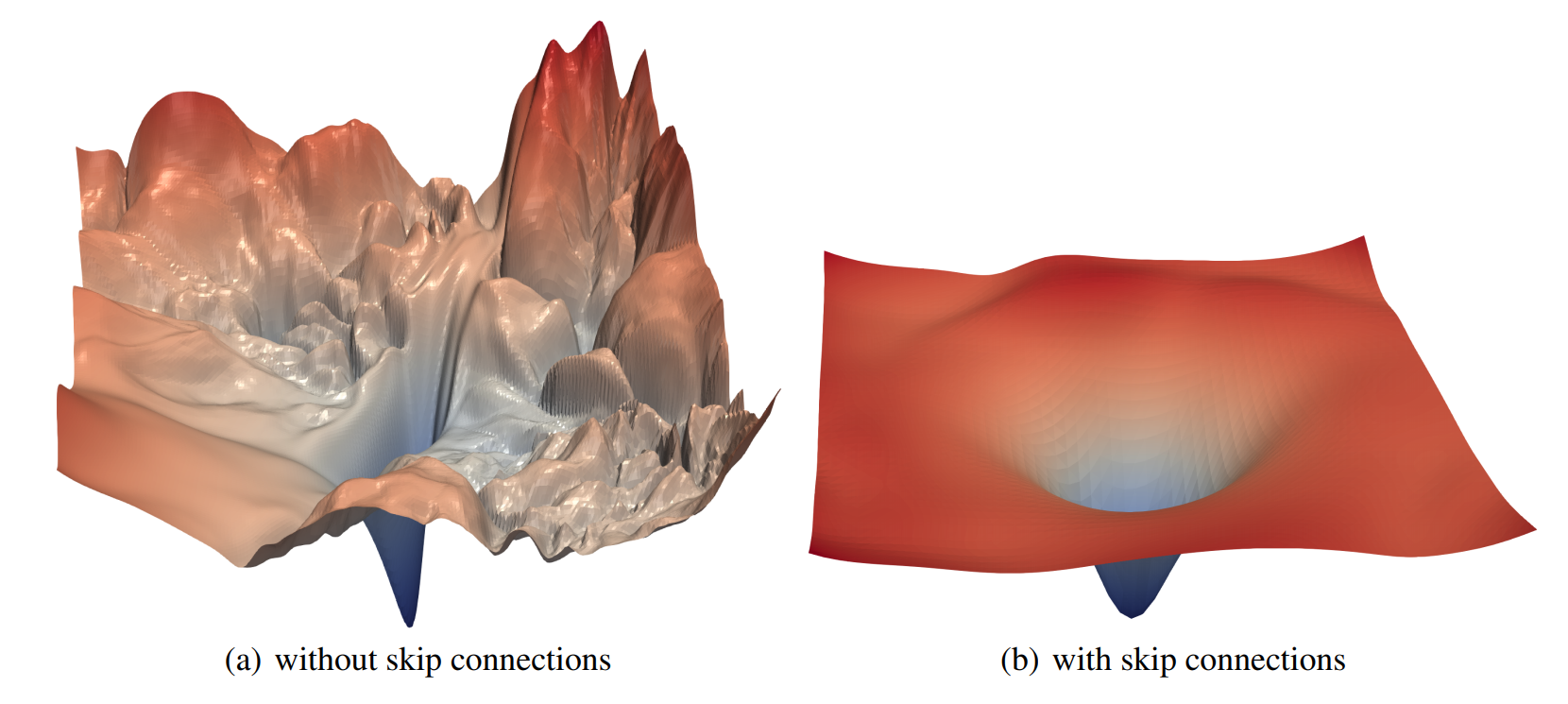
Grokking refers to a delayed generalization following overfitting when optimizing artificial neural networks with gradient-based methods. We show that the dynamic of grokking goes beyond the $\ell_2$ norm, that is: If there exists a model with a property $P$ (e.g., sparse or low-rank weights) that fits the data, then GD with a small (explicit or implicit) regularization of $P$ (e.g., $\ell_1$ or nuclear norm regularization) will also result in grokking, provided the number of training samples is large enough. Moreover, the $\ell_2$ norm of the parameters is no longer guaranteed to decrease with generalization when it is not the property sought.

Paper : Grokking Beyond the Euclidean Norm of Model Parameters, Pascal Jr. Tikeng Notsawo, Guillaume Dumas, Guillaume Rabusseau, Forty-Second International Conference on Machine Learning (ICML), 2025. https://arxiv.org/abs/2506.05718

Blog post : https://hackmd.io/@6LQ4mvRtS4Sc3LHkNEvDXQ/BytCby2Ugl

You May Also Enjoy

Epoch-wise bias-variance decomposition

14 minute read

Published:

Let’s suppose we’re training a model parameterized by $\theta$, and let’s denote by $\theta_t$ the parameter $\theta$ at step $t$ given by the optimization algorithm of our choice. In machine learning, it is often helpful to be able to decompose the error $E(\theta)$ as $B^2(\theta)+V(\theta)+N(\theta)$, where $B$ represents the bias, $V$ the variance, and $N$ the noise (irreducible error). In most cases, the decomposition is performed on an optimal solution $\theta^*$ (for instance, $\lim_{t \rightarrow \infty} \theta_t$, or its early stopping version), for example, in order to understand how the bias and variance change with the complexity of the function implementing $\theta$, the size of this function, etc. This has helped explain phenomena such as model-wise double descent. On the other hand, it can also be interesting to visualize how $B(\theta_t)$ and $V(\theta_t)$ evolve with $t$ (which can help explain phenomena like epoch-wise double descent): that’s what we’ll be doing in this blog post.