Pascal Jr. Tikeng Notsawo

Pascal Jr. Tikeng Notsawo

PhD Student at UdeM & Mila

Posts by Tags

Acceptance-Rejection Method

Bag of words

GflowNets

Gibbs sampling

Glove

Important Sampling

Inverse Transform Sampling

MCMC

Metropolis-Hasting

Metropolis-adjusted Langevin

NLP

TF-IDF

Word2Vec

bias-variance tradeoff

Epoch-wise bias-variance decomposition

14 minute read

Published:

Let’s suppose we’re training a model parameterized by $\theta$, and let’s denote by $\theta_t$ the parameter $\theta$ at step $t$ given by the optimization algorithm of our choice. In machine learning, it is often helpful to be able to decompose the error $E(\theta)$ as $B^2(\theta)+V(\theta)+N(\theta)$, where $B$ represents the bias, $V$ the variance, and $N$ the noise (irreducible error). In most cases, the decomposition is performed on an optimal solution $\theta^*$ (for instance, $\lim_{t \rightarrow \infty} \theta_t$, or its early stopping version), for example, in order to understand how the bias and variance change with the complexity of the function implementing $\theta$, the size of this function, etc. This has helped explain phenomena such as model-wise double descent. On the other hand, it can also be interesting to visualize how $B(\theta_t)$ and $V(\theta_t)$ evolve with $t$ (which can help explain phenomena like epoch-wise double descent): that’s what we’ll be doing in this blog post.

deep learning

Epoch-wise bias-variance decomposition

14 minute read

Published:

Let’s suppose we’re training a model parameterized by $\theta$, and let’s denote by $\theta_t$ the parameter $\theta$ at step $t$ given by the optimization algorithm of our choice. In machine learning, it is often helpful to be able to decompose the error $E(\theta)$ as $B^2(\theta)+V(\theta)+N(\theta)$, where $B$ represents the bias, $V$ the variance, and $N$ the noise (irreducible error). In most cases, the decomposition is performed on an optimal solution $\theta^*$ (for instance, $\lim_{t \rightarrow \infty} \theta_t$, or its early stopping version), for example, in order to understand how the bias and variance change with the complexity of the function implementing $\theta$, the size of this function, etc. This has helped explain phenomena such as model-wise double descent. On the other hand, it can also be interesting to visualize how $B(\theta_t)$ and $V(\theta_t)$ evolve with $t$ (which can help explain phenomena like epoch-wise double descent): that’s what we’ll be doing in this blog post.

loss landscape

statistical learning

Epoch-wise bias-variance decomposition

14 minute read

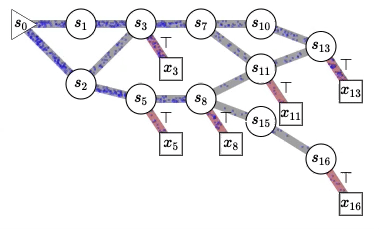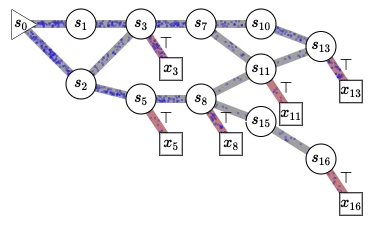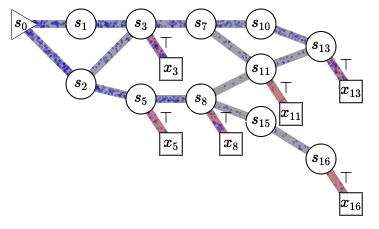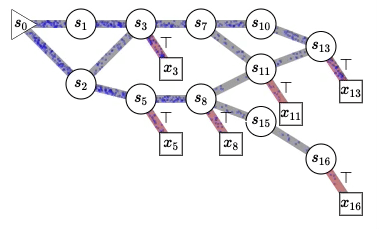
Published:

Let’s suppose we’re training a model parameterized by $\theta$, and let’s denote by $\theta_t$ the parameter $\theta$ at step $t$ given by the optimization algorithm of our choice. In machine learning, it is often helpful to be able to decompose the error $E(\theta)$ as $B^2(\theta)+V(\theta)+N(\theta)$, where $B$ represents the bias, $V$ the variance, and $N$ the noise (irreducible error). In most cases, the decomposition is performed on an optimal solution $\theta^*$ (for instance, $\lim_{t \rightarrow \infty} \theta_t$, or its early stopping version), for example, in order to understand how the bias and variance change with the complexity of the function implementing $\theta$, the size of this function, etc. This has helped explain phenomena such as model-wise double descent. On the other hand, it can also be interesting to visualize how $B(\theta_t)$ and $V(\theta_t)$ evolve with $t$ (which can help explain phenomena like epoch-wise double descent): that’s what we’ll be doing in this blog post.